TERCEIRA QUANTIZAÇÃO PELO SDCTIE GRACELI

TRANS-QUÂNTICA SDCTIE GRACELI, TRANSCENDENTE, RELATIVISTA SDCTIE GRACELI, E TRANS-INDETERMINADA.

FUNDAMENTA-SE EM QUE TODA FORMA DE REALIDADE SE ENCONTRA EM TRANSFORMAÇÕES, INTERAÇÕES, TRANSIÇÕES DE ESTADOS [ESTADOS DE GRACELI], ENERGIAS E FENÔMENOS DENTRO DE UM SISTEMA DE DEZ OU MAIS DIMENSÕES DE GRACELI, E CATEGORIAS DE GRACELI.

FUNÇÃO GERAL GRACELI DA TRANS- INDETERMINALIDADE PELO SDCTIE GRACELI

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE  INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.  E DE ESTADOS TRANSICIONAIS =

TRANSFORMAÇÕES ⇔ INTERAÇÕES  ⇔  TUNELAMENTO ⇔ EMARANHAMENTO ⇔ CONDUTIVIDADE  ⇔ DIFRAÇÕES ⇔ estrutura eletrônica, spin, radioatividade, ABSORÇÕES E EMISSÕES INTERNA ⇔  Δ de temperatura e dinâmicas, transições de estados quântico Δ ENERGIAS,  ⇔   Δ MASSA ,   ⇔ Δ  CAMADAS ORBITAIS ,  ⇔  Δ FENÔMENOS  ,  ⇔  Δ  DINÂMICAS,   ⇔  Δ  VALÊNCIAS,   ⇔  Δ BANDAS,  Δ  entropia e de entalpia,  E OUTROS.  

x

 [EQUAÇÃO DE DIRAC].

 + FUNÇÃO TÉRMICA.

   +    FUNÇÃO DE RADIOATIVIDADE

  ,      +   FUNÇÃO DE TUNELAMENTO QUÂNTICO.

  + ENTROPIA REVERSÍVEL 

+      FUNÇÃO DE CONDUÇÃO ELETROMAGNÉTICA

 ENERGIA DE PLANCK

X

• 
  V [R] [MA] =  Δe,M, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM......

  ΤDCG

  X

  Δe, ΔM, Δf, ΔE, Δt, Δi, ΔT, ΔC, ΔE,ΔA, ΔD, ΔM......  =
  x
  

  sistema de dez dimensões de Graceli + 

  DIMENSÕES EXTRAS DO SISTEMA DECADIMENSIONAL E CATEGORIAL GRACELI.[como, spins, posicionamento, afastamento, ESTRUTURA ELETRÔNICA, e outras já relacionadas]..
• 
  
• DIMENSÕES DE FASES DE ESTADOS DE TRANSIÇÕES DE GRACELI.
  

  x

  sistema de transições de estados, e estados  de Graceli, fluxos aleatórios quântico, potencial entrópico e de entalpia. [estados de transições de fases de estados de estruturas, quântico, fenomênico, de energias, e dimensional [sistema de estados de Graceli].

  x

número atômico, estrutura eletrônica, níveis de energia 

[comprimento de onda (λ).

onde c, velocidade da luz, é igual a .]

X

• TEMPO ESPECÍFICO E FENOMÊNICO DE GRACELI.
• X
• CATEGORIAS DE GRACELI
• T l    T l     E l       Fl         dfG l   

  N l    El                 tf l

  P l    Ml                 tfefel 

  Ta l   Rl

           Ll  *  D
           

X

 [ESTADO QUÂNTICO]

Na física e na ciência dos materiais, a Temperatura de Curie (T_c), ou o Ponto de Curie, é a temperatura na qual o magnetismo permanente de um material se torna um magnetismo induzido. A força do magnetismo é determinada pelo momento magnético.

A temperatura de Curie é o ponto crítico onde o momento magnético intrínseco do material muda de direção. Momentos magnéticos são momentos de dipolo permanentes que dentro do átomo são criados a partir do momento angular e do spin dos elétrons. Materiais tem diferentes estruturas de momentos magnéticos intrínsecos que variam com a mudança de temperatura.

Magnetismo permanente é causado pelo alinhamento dos momentos magnéticos e magnetismo induzido é criado quando momentos magnéticos desordenados são forçados a se alinhar em um campo magnético requerido. Por exemplo, os momentos magnéticos ordenados (ferromagnético, Figura 1) mudam e se tornam desordenados (paramagnético, Figura 2) na Temperatura de Curie.

Altas temperaturas fazem a magnetização espontânea de imãs mais fracos ocorrer apenas na Temperatura de Curie. Susceptibilidade magnética só ocorre acima da Temperatura de Curie e pode ser calculada pela Lei de Curie-Weiss que é derivada da Lei de Curie.

Em analogia aos materiais ferromagnéticos e paramagnéticos, a temperatura de Curie pode ser usada para descrever a temperatura onde polarização eletrostática espontânea do material se torna um polarização eletrostática induzida ou o contrário caso a temperatura seja reduzida abaixo da Temperatura de Curie.

A Temperatura de Curie recebeu esse nome depois que Pierre Curie mostrou que o magnetismo se perde depois de alcançar uma temperatura crítica.^[1]

Temperatura Curie dos Materiais^[2][3][4]

Material	Temperatura de Curie (°C)
Ferro (Fe)	770
Cobalto (Co)	1127
Níquel (Ni)	354
Gadolínio (Gd)	19
Disprósio (Dy)	-185
MnBi	357
MnSb	314
CrO2	113
MnAs	45
EuO	-204
Óxido férrico (Fe2O3)	675
Óxido de ferro(II,III) (FeOFe2O3)	585
NiOFe2O3	585
CuOFe2O3	455
MgOFe2O3	440
MnOFe2O3	300
Y3Fe5O12	287
Ímã de neodímio	310-400
Alnico	700-860
Imã Samário-Cobre	720-800
Ferrite	450

Lei de Curie-Weiss

A Lei de Curie-Weiss é uma versão 

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE  INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.  E DE ESTADOS TRANSICIONAIS

adaptada da Lei de Curie.

A Lei de Curie-Weiss é um modelo simples derivado da aproximação do campo médio, isso significa que funciona bem quando a temperatura do material,T, é muito maior que sua correspondente Temperatura de Curie,T_c, logo T >> T_c; Entretanto falha para descrever a susceptibilidade magnética, χ, na proximidade imediata do ponto de Curie por causa das flutuações locais entre os átomos.^[5]

Ambas Lei de Curie e Lei de Curie-Weiss não servem quando T< T_c.

Lei de Curie para material paramagnético:^[6]

${\displaystyle \chi ={\frac {M}{H}}={\frac {M\mu _{0}}{B}}={\frac {C}{T}}}$

X

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE  INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.  E DE ESTADOS TRANSICIONAIS

Definition
χ	a susceptibilidade magnética; influência de um campo magnético requerido no material
M	momento magnético por unidade de volume
H	o campo magnético macroscópico
B	o campo magnético
C	a Constante Curie específica do material

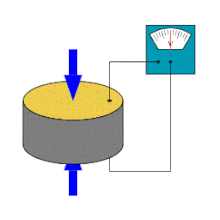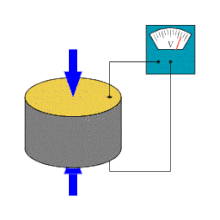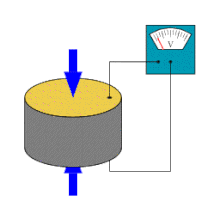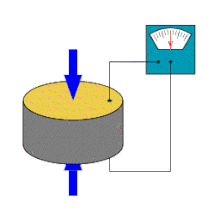
Piezoeletricidade é a capacidade de alguns cristais gerarem tensão elétrica por resposta a uma pressão mecânica. O termo piezoeletricidade provém do grego piezein, que significa apertar/pressionar. Referente à geração de corrente elétrica, juntou-se a designação eletricidade, de modo que piezoeletricidade é interpretado como a produção de energia elétrica devido à compressão sobre determinados materiais.

Mecanismo

Um disco piezoelétrico gera uma diferença de potencial quando deformado.

O efeito piezoelétrico é entendido como a interação eletromecânica linear entre a força mecânica e o estado elétrico (forças de Coulomb) em materiais cristalinos (cerâmicos, polímeros).

O efeito piezoelétrico é um processo reversível em que os materiais exibem o efeito piezoelétrico direto (a geração interna de carga elétrica resultante de uma força mecânica aplicada), mas também exibem o efeito piezoelétrico reverso (a geração interna de uma tensão mecânica resultante de um campo elétrico aplicado). Por exemplo, os cristais de titanato zirconato de chumbo irão gerar piezoeletricidade mensurável quando a sua estrutura estática é deformada por cerca de 0,1% da dimensão inicial. Por outro lado, esses mesmos cristais mudam cerca de 0,1% da sua dimensão estática quando um campo elétrico externo é aplicado ao material. Como exemplo, o efeito piezoelétrico inverso é usado na produção de ondas de ultrassom.^[1]

Cristais

Utilizando argumentos referentes à simetria, o efeito piezoelétrico não existe em materiais que apresentam simetria central, e desta forma, podem ser polarizados, ou seja, a piezoeletricidade pode ser explicada pela assimetria de polarização iônica. Porém, elementos puros, tais como selênio (Se) e telúrio (Te) também exibem a propriedade de piezoeletricidade. Nestes casos, a polarização elétrica induzida é atribuída à distribuição eletrônica, que é alterada pela ação externa.

Considerando as trinta e duas classes de cristais catalogadas, 21 não são centrossimétricas (não possuem centro de simetria); vinte destes exibem piezoeletricidade direta; dez destes representam as classes de cristal polares, que mostram uma polarização espontânea, sem estresse mecânico devido a um momento de dipolo elétrico permanente. Se o momento de dipolo puder ser revertido por meio da aplicação de um campo elétrico externo, então o material é considerado ferroelétrico.

Para cristais polares, para os quais o momento de dipolo P diferente de zero se mantém sem se aplicar uma carga mecânica, o efeito piezoelétrico manifesta-se alterando a magnitude ou a direção do vetor momento de dipolo ou ambos. Para os cristais não-polares, mas piezoelétricos, a polarização diferente de zero é apenas induzida pela aplicação de uma carga mecânica. Para eles, a tensão pode ser imaginada para transformar o material a partir de uma classe de cristal não polar (P = 0) para uma polar, para a qual P ≠ 0.

A maioria dos cristais não possui propriedades piezoelétricas. O mais importante cristal natural que possui esta propriedade é o quartzo. Além deste, pela facilidade de sintetização, os cristais utilizados são cerâmicas à base de, por exemplo, titanato de bário ou zirconato de chumbo.^[2]

Descrição matemática

A piezoelectricidade é uma combinação de efeitos do comportamento elétrico do material:^[3]

$${\displaystyle D=\varepsilon E+eS\;}$$

X

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE  INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.  E DE ESTADOS TRANSICIONAIS

Nessa equação, D é o deslocamento elétrico, ε é a permissividade elétrica, E representa o campo elétrico, 'e' representa a constante de stress e S é a tensão longitudinal aplicada.

Quando a aplicação de uma força F, o centro de equilíbrio das cargas positivas e negativas é deslocado, causando a polarização do material, e o consequente deslocamento de corrente.

Similarmente, considerações para o caso quando um campo elétrico E é aplicado mostram que um termo referente a stress adicional, -eE, aparece. Tem-se então a Lei de Hooke, T = cS:

$${\displaystyle T=cS-eE\;}$$

X

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE  INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.  E DE ESTADOS TRANSICIONAIS

Se as cargas de moléculas positivas e negativas possuem magnitudes diferentes, há uma polarização espontânea. Se uma molécula possui um momento de dipolo, este material exibe uma polarização iônica. Já no caso onde há somente um tipo de elemento, mas este é polarizável, temos o efeito de polarização eletrônica.

A piezoeletricidade apresenta relação entre propriedades elétricas (E, D) e mecânicas (S, T). O modelo de um sólido piezoelétrico apresenta quatro diferentes relações entre variáveis. Assumimos que ${\displaystyle T=T(S,E)}$ e ${\displaystyle D=D(S,E)}$. Assim, temos

$${\displaystyle dT=\left({\frac {\partial T}{\partial S}}\right)dS+\left({\frac {\partial T}{\partial E}}\right)dE}$$

X

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE  INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.  E DE ESTADOS TRANSICIONAIS

$${\displaystyle dD=\left({\frac {\partial D}{\partial S}}\right)dS+\left({\frac {\partial D}{\partial E}}\right)dE}$$

X

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE  INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.  E DE ESTADOS TRANSICIONAIS

onde todos os outros efeitos, tais como magnéticos e térmicos, assim como termos não-lineares, são ignorados.

Considerando o caso onde ao campo elétrico é aplicado sobre o material piezoelétrico (ao se colocar um material piezoelétrico num campo elétrico externo, as cargas elétricas da rede cristalina interagem com o mesmo e produzem tensões mecânicas), os segundos termos das equações acima enunciam o stress ou a tensão elétrica no material. Se o material não está confinado mecanicamente, a tensão será uma força de reação a força imposta pelo stress. Desta forma, a tensão altera a relação D e E, e assim a medição das propriedades elétricas dependentes das propriedades mecânicas. Do mesmo modo, uma tensão elétrica alterará a medição de propriedades mecânicas dependentes das propriedades elétricas. Em ambos os casos, isso demonstra a essência do acoplamento piezoelétrico. Para uma análise mais detalhada, deve-se comparar diferentes materiais piezoelétricos para identificar sua performance. Fatores como a eficiência do acoplamento a vibrações mecânicas, vibrações com campos elétricos externos, direção de aplicação do campo elétrico externo e demais, são resultados a serem considerados.

Num material piezoelétrico também interessam os seguintes coeficientes:

• Coeficiente de acoplamento eletro-mecânico:

${\displaystyle K^{2}}$ é definido como a variação de energia mecânica convertida em carga pela energia mecânica aplicada ao cristal, ou de modo similar, a energia elétrica convertida em energia mecânica pela energia elétrica aplicada ao cristal.

• Coeficiente Dielétrica: esta grandeza relaciona a quantidade de carga que uma das faces do cristal pode armazenar em relação à carga total armazenada, e que pode ser dissipada como corrente real. Existem duas constantes dielétricas: uma é a constante para o cristal livre e outra para o cristal bloqueado:

${\displaystyle \varepsilon _{l}(1-K^{2})=\varepsilon _{b}}$

X

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE  INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.  E DE ESTADOS TRANSICIONAIS

Em física, termodinâmica, química, físico-química e física da matéria condensada, um ponto crítico, também chamado de estado crítico, ocorre sob condições (tais como valores específicos de temperatura, pressão ou composição) no qual não existem limites de fase. Existem vários tipos de pontos críticos, incluindo pontos críticos líquido-vapor e líquido-líquido.^[1][2]

Substâncias puras: ponto crítico líquido-vapor

O "ponto crítico" é por vezes usado para denotar o ponto especificamente vapor-líquido crítico de um material, a partir do qual a distinção entre fase a líquida e gasosa não existe.

O ponto crítico de vapor-líquido em um diagrama de fases pressão-temperatura está no extremo de alta temperatura do limite de fase líquido-gás. A linha pontilhada verde mostra o comportamento anômalo da água.^[3]

Como se mostra no diagrama de fases para a direita, isto é o ponto em que a fronteira entre a fase líquida e gasosa termina. Em água, o ponto crítico ocorre em cerca de 647 K. (374 ° C; 705 ° F) e 22,064 MPa (218 atm)

À medida que a substância se aproxima da temperatura crítica, as propriedades da sua fases gasosa e líquida convergem, resultando em apenas uma fase no ponto crítico: um fluido supercrítico homogêneo. O calor de vaporização é zero no ponto crítico e para além dele, por isso não existe distinção entre as duas fases. No diagrama de Pressão-temperatura, o ponto em que a temperatura crítica e pressão crítica satisfazer é chamado de ponto crítico da substância. Acima da temperatura crítica, um líquido não pode ser formada por um aumento da pressão, apesar de um sólido poder ser formado sob uma pressão suficiente. A pressão crítica é a pressão de vapor, à temperatura crítica. O volume crítico é o volume molar de uma mole do material a uma temperatura e pressão críticas.

Propriedades críticas variam de material para material, e para muitas substâncias puras estão prontamente disponíveis na literatura. No entanto, a obtenção de propriedades críticas para misturas é mais desafiador.

Definição matemática

No caso das substâncias puras, há um ponto de inflexão na curva isotérmica crítica (linha de temperatura constante) com um diagrama de Pressão-Volume. Isto significa que, no ponto crítico: ^[4][5][6]

${\displaystyle \left({\frac {\partial p}{\partial V}}\right)_{T}=\left({\frac {\partial ^{2}p}{\partial V^{2}}}\right)_{T}=0}$

X

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE  INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.  E DE ESTADOS TRANSICIONAIS

Isto é, as primeira e segunda derivadas parciais da pressão p no que diz respeito ao volume V são ambos zero, com as derivadas parciais avaliados em temperatura constante T. Esta relação pode ser usada para avaliar dois parâmetros de uma equação de estado em termos das propriedades críticas, tais como os parâmetros a e b na equação de van der Waals.^[4]

Às vezes um conjunto de propriedades reduzidas é definida em termos das propriedades importantes, isto é:^[7]

${\displaystyle T_{r}=T/T_{c}\,}$

X

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE  INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.  E DE ESTADOS TRANSICIONAIS

${\displaystyle p_{r}=p/p_{c}\,}$

X

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE  INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.  E DE ESTADOS TRANSICIONAIS

${\displaystyle V_{r}={\frac {V}{RT_{c}/p_{c}}}\,}$

X

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE  INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.  E DE ESTADOS TRANSICIONAIS

${\displaystyle T_{c}=8a/27Rb,}$

X

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE  INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.  E DE ESTADOS TRANSICIONAIS

${\displaystyle V_{c}=3b\,}$

X

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE  INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.  E DE ESTADOS TRANSICIONAIS

${\displaystyle P_{c}=a/27b^{2},}$

X

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE  INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.  E DE ESTADOS TRANSICIONAIS

onde ${\displaystyle T_{r}}$ é a temperatura reduzida, ${\displaystyle p_{r}}$ é a pressão reduzida, ${\displaystyle V_{r}}$ é a redução do volume, e ${\displaystyle R}$ é a constante universal dos gases.

Proposta pelo físico estadunidense Josiah Willard Gibbs, a Regra das Fases de Gibbs apresenta um critério para a determinação das fases que coexistirão em um sistema em equilíbrio num diagrama de fase.^[1]

Definição

A regra das fases de Gibbs é expressa pela equação

${\displaystyle P+F=C+N}$ ,

X

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE  INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.  E DE ESTADOS TRANSICIONAIS

em que P é o número de fases presentes, F é o número de graus de liberdade, ou o número de variáveis que podem ser controladas externamente, e que devem ser especificadas para definir por completo o estado de um sistema. O parâmetro C representa o número de componentes e N é o número de variáveis não relacionadas à composição. Como muitas vezes essas variáveis são a temperatura e a pressão, é comum a equação aparecer como:

${\displaystyle P+F=C+2}$ .

X

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE  INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.  E DE ESTADOS TRANSICIONAIS

Sistema unário

Para sistemas com um só componente, em que C = 1 e as variáveis são temperatura e pressão, de modo que N = 2, a equação toma a forma

${\displaystyle P+F=3}$ .

X

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE  INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.  E DE ESTADOS TRANSICIONAIS

No ponto triplo coexistem três fases em equilíbrio. Como há apenas um componente, o número de graus de liberdade é dado por

${\displaystyle F=C+N-P}$

${\displaystyle P=1+2-3}$

X

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE  INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.  E DE ESTADOS TRANSICIONAIS

ou seja, F = 0. Isso significa que nenhuma variável (temperatura ou pressão) pode ser mudada, mantendo-se a existência das três fases.

Ao longo de um contorno de fase, duas fases estão em equilíbrio, de modo que

${\displaystyle P=1+2-2}$

X

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE  INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.  E DE ESTADOS TRANSICIONAIS

e há apenas um grau de liberdade. Isso significa que para descrever o estado basta especificar apenas uma das variáveis, pois a outra já está definida.

Considerando um ponto situado em uma região com apenas uma fase,

${\displaystyle P=1+2-1}$

o número de graus de liberdade nesse caso é 2. São necessárias duas variáveis para definir o estado do sistema.

Sistema binário

Para misturas binárias, há dois componentes (C = 2) e, além da temperatura e pressão, há a presença do grau de liberdade composição. Como muitas vezes as operações metalúrgicas, que fazem uso do diagrama binário, são realizadas à pressão atmosférica, a pressão é dada como constante a 1 atm, de modo que N = 1.^[2]

${\displaystyle F=C-P+1}$

X

FUNÇÃO FUNDAMENTAL E GERAL DO SISTEMA [SDCTIE GRACELI] DE  INTERAÇÕES, TRANSFORMAÇÕES EM CADEIAS, DECADIMENSIONAL E CATEGORIAL GRACELI.  E DE ESTADOS TRANSICIONAIS